This is a bit of a trick question. For the modern age the question would have been better phrased as either "What answer should your calculator give you when you push these keys ?" or "If this was an Excel formula, what would be the answer ?"
For extra credit this is how to get the various answers: Work out the bits in the innermost ( brackets ) first. (second bit ( first bit ))
0=(7+7)/(7+7)*(7-7)
8=(7+(7/(7+(7*(7-7)))))
50=7+7/7+7*7-7
50=7+(7/7)+(7*7)-7
56==((((7+7)/7)+7)*7)-7
The highlighted answers give the "correct" method to work out the answer. Parts of a sum in ( ) must be worked out first, followed by all * and / only then can the + and - be evaluated. Breaking this down we get
7+7/7+7*7-7
There are not brackets so we first work out the 7/7 and 7*7
7+ 1 + 49 - 7
which becomes
8 + 42
= 50
Some "bad" calculators, will incorrectly give the answer 56 because they jump to the partial answers after each time any of the + - * / keys are pushed.
7+7 = 14
/ 7 = 2
+ 7 = 9
* 7 = 63
- 7 = 56
The answer to why the "bad" calculator method is wrong comes from the basic rule that the order that a sum is written should not make a difference to the answer.
2 + 1 / 2 must be the same as 1 / 2 + 2 read this as
Two plus a half is equal to two plus a half.
Two plus a half is equal to a half plus two.
A "bad" calculator would read 2 + 1 / 2 as
Two plus one is three, divided by two equals one and a half.
There are more ways to get wrong answers from the sum above if the order of execution is adjusted. Work out the parts in brackets first :
44=(7+7)/7+(7*7)-7
2=(7+7)/7+7*(7-7)
0.2857=(7+7)/(7+7*7-7)
-6.75=(7+7)/(7+7*7)-7
With so many possible choices for a simple sum there has to be agreement on how to calculate any written sum. Having two people work out the same written sum in different ways is the road to math madness. Luckily this has been mostly resolved. See Google "Bodmas" or order of operations more detailed explanations.
How did "bad" calculators come about ? Back in history when calculators were mechanical they only had a single "running total" displayed. Each operation immediately changed the running total without reference to the previous operations. Such calculator users were expected to reorder the operations before using the calculator. The early electronic calculator followed this methodology.
Fun
Just for fun, here is how various professions would tackle this question. What is closest to your way of thinking ?
- Mathematician – There are at least 8 possible answers depending on …..
- Scientist – I asked 500 people the same question and they said …..
- Engineering – The answer has been calculated in Excel, on a Calculator, with a slide-rule, on paper and in my head as …
- Teacher – We can find the answer by following this method ….
- Lawyer – What do the books say the answer is ?
- Philosopher – First we must understand how we relate to the concept of 7 in this context.
- Graphics designer – The spacing between the symbols is inconsistent, and the font does not match, resulting in ambiguity and confusion.
- PR consultant – Whatever the client wants is The Answer.
- Media Guru – Call 0907834348* to get the answer. *( 75p/Min + call charges apply )
**Update April 2020 **
Find out how to solve Sudoku and Giant Sudoku variants using a logic solver here
See also :
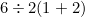
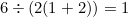
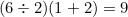
3 comments:
A "bad" calculator would still give 2 1/2 or 2.5
2 + 0.5 = 2.5 whichever way round you write it.
2 + 1 / 2 versus 1 / 2 + 2 will give a different answers on non-scientific calculators.
C is answer
Post a Comment